1. 概述
红黑树(Red–black tree)是一种平衡二叉查找树,它可以在 O(logn)时间内完成查找,插入和删除,这里的n是树中元素的数目,我们首先介绍下二叉查找树。
二叉查找树(Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
在理想的情况下,二叉查找树插入、删除、查询的时间复杂度为O(logn),最坏的情况下为O(N)。如果插入的数据是有序的情况下,二叉查找树会出现倾斜,退化为链表,如下图所示: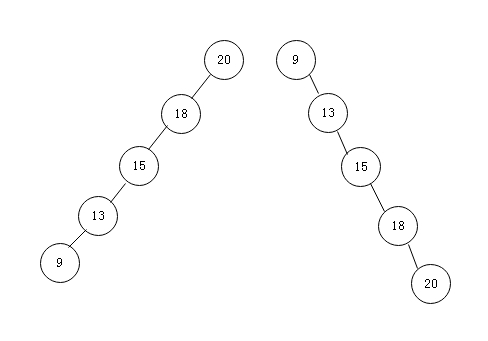
为了解决倾斜的问题,引入了平衡二叉查找树,AVL和红黑树是其两种类型,它们都能保证在时间复杂度为O(logn)下实现二叉查找树的增删查。
在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(logn)。插入和删除元素的操作需要进行一次或多次旋转,以实现树的重新平衡,实际上插入操作最多两次旋转,而删除操作需要最多O(logn)次旋转。
红黑树相对于AVL树来说,牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树。在红黑树中,进行插入操作和删除操作只需要少量O(logn)的颜色变更和不超过三次树旋转(对于插入操作是两次),虽然插入和删除很复杂,但操作时间仍可以保持为O(logn)次。
红黑树的实际应用非常广泛,比如Linux内核中的完全公平调度器、高精度计时器、ext3文件系统等等,各种语言的函数库如Java的TreeMap和TreeSet,C++ STL的map、multimap、multiset等等。
红黑树的插入和删除操作相对来说还是比较复杂,为了简化算法,引入了一种新的数据结构跳跃表(Skip List)。Skip List是一种随机化的数据结构,基于并联的链表,其效率可比拟于二叉查找树(对于大多数操作需要O(logn)平均时间)。跳跃列表的插入和删除的实现与普通的链表操作类似,相对比较简单,但高层元素必须在进行多个链表中进行插入或删除。
跳跃列表的发明者对跳跃列表的评价是:“跳跃列表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃列表的算法有同平衡树一样的渐进的预期时间边界,并且更简单、更快速和使用更少的空间。”,跳跃表的一个应用场景是作为Redis有序集合对象的底层实现,跳跃表将在后面的文章中讲述。
现在对这几种数据结构做一个比较对比: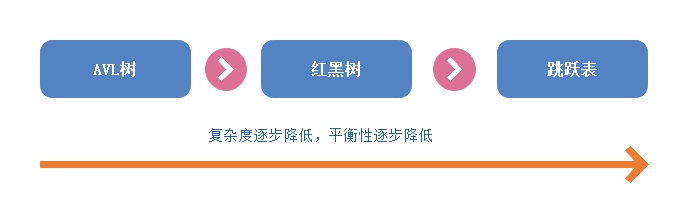
2. 概念
2.1 定义
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。其特点如下:
- 1)节点是红色或黑色;
- 2)根是黑色;
- 3)所有叶子都是黑色的(叶子是NIL节点);
- 4)每个红色节点必须有两个黑色的子节点(从每个叶子到根的所有路径上不能有两个连续的红色节点);
- 5)从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
这些约束确保了红黑树的关键特性:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的。
要知道为什么这些性质确保了这个结果,注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
下图就是一个红黑树的图例,来自维基百科。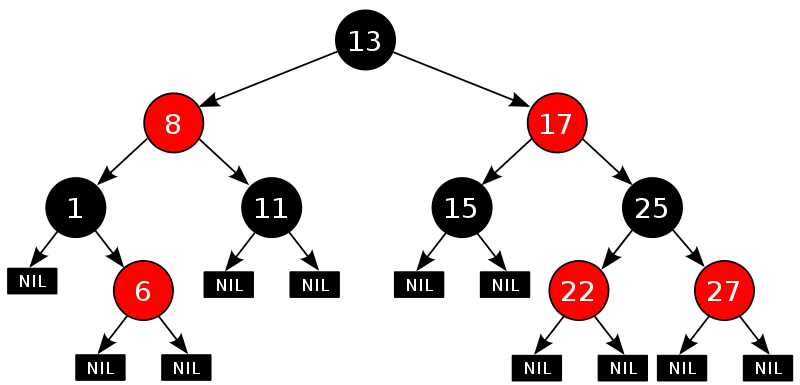
叶子结点用NIL节点表示。
红黑树的结构跟二叉查找树结构类型,在其基础上用一个属性来表示结点的颜色。代码定义如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public class RBTree<T extends Comparable<T>> {
private RBNode<T> root; // 根结点
private static final boolean RED = false;
private static final boolean BLACK = true;
// 结点定义
private class RBNode<T extends Comparable<T>> {
boolean color; // 颜色
T key; // 键值
RBNode<T> left; // 左结点
RBNode<T> right; // 右结点
RBNode<T> parent; // 父结点
...
}
...
}
对红黑树进行插入及删除操作时,会改变红黑树的平衡,需要通过变色、左旋及右旋三种操作来修正,使其满足红黑树的定义。
2.2 变色
变色操作比较简单,代价也比较代,只是对结点的赋值操作,代码如下所示:1
2
3
4
5
6
7
8
9
10
11public void setRed(RBNode<T> node) {
if (node != null) {
node.color = RED;
}
}
public void setBlack(RBNode<T> node) {
if (node != null) {
node.color = BLACK;
}
}
2.3 左旋
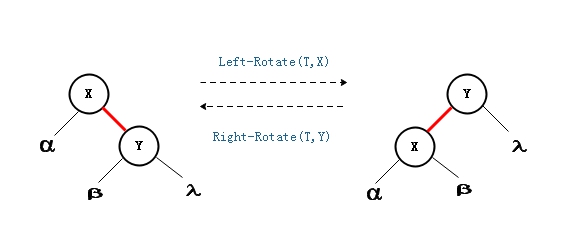
如下图所示,左旋是X到Y的结点为“支轴”进行,它使X的右孩子Y成为该子树的新的根,X成为Y的左孩子,Y的左孩子成为X的右孩子。右旋与左旋是对称的操作,Y的左孩子X成为新子树的根,Y成为X的右孩子,X之前的右孩子成为Y的右孩子,下面的动图形象的展示了左旋的过程。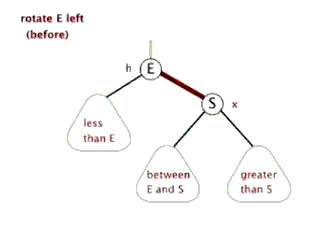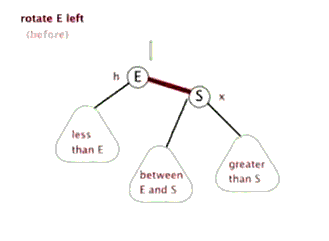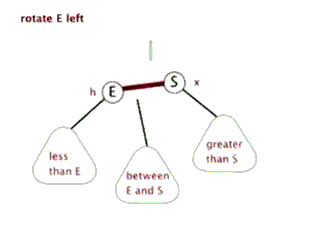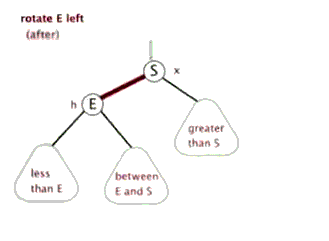
左旋的代码如下所示:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38/*
* 左旋示意图:对节点x进行左旋
* p p
* / /
* x y
* / \ / \
* lx y -----> x ry
* / \ / \
* ly ry lx ly
*
*/
private void leftRotate(RBNode<T> x) {
RBNode<T> y = x.right;
RBNode<T> parent = x.parent;
// 1. 将y的左子节点赋给x的右子节点,并将x赋给y左子节点的父节点(y左子节点非空时)
x.right = y.left;
if (y.left != null) {
y.left.parent = x;
}
// 2. 将x的父节点p(非空时)赋给y的父节点,同时更新p的子节点为y(左或右)
y.parent = parent;
if (parent == null) {
this.root = y;
} else {
if (parent.left == x) {
parent.left = y;
} else {
parent.right = y;
}
}
// 3.将y的左子节点设为x,将x的父节点设为y
y.left = x;
x.parent = y;
}
左旋做了三件事:
- 1)将y的左子节点赋给x的右子节点,并将x赋给y左子节点的父节点(y左子节点非空时);
- 2)将x的父节点p(非空时)赋给y的父节点,同时更新p的子节点为y(左或右);
- 3)将y的左子节点设为x,将x的父节点设为y。
2.4 右旋
根据上面的描述我们可以知道,右旋与左旋是对称的操作,下面的动图形象地展示了右旋的过程。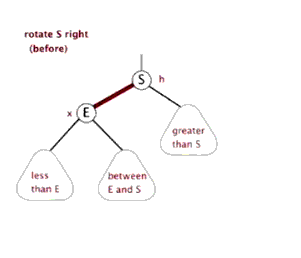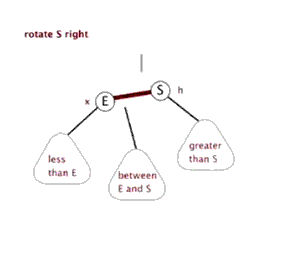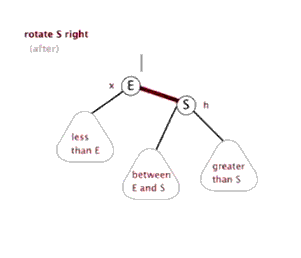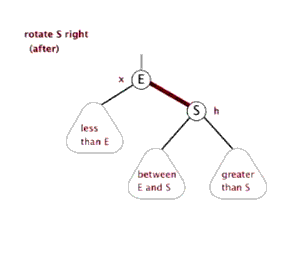
右旋的代码如下所示:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38/*
* 右旋示意图:对节点y进行右旋
* p p
* / /
* y x
* / \ / \
* x ry -----> lx y
* / \ / \
* lx rx rx ry
*
*/
private void rightRotate(RBNode<T> y) {
RBNode<T> x = y.left;
RBNode<T> parent = y.parent;
// 1. 将x的右子节点赋给y的左子节点,并将y赋给x右子节点的父节点(x右子节点非空时)
y.left = x.right;
if (x.right != null) {
x.right.parent = y;
}
// 2. 将y的父节点p(非空时)赋给x的父节点,同时更新p的子节点为x(左或右)
x.parent = parent;
if (parent == null) {
this.root = x;
} else {
if (parent.left == y) {
parent.left = x;
} else {
parent.right = x;
}
}
// 3. 将x的右子节点设为y,将y的父节点设为x
x.right = y;
y.parent = x;
}
右旋做了三件事:
- 1)将x的右子节点赋给y的左子节点,并将y赋给x右子节点的父节点(x右子节点非空时);
- 2)将y的父节点p(非空时)赋给x的父节点,同时更新p的子节点为x(左或右);
- 3)将x的右子节点设为y,将y的父节点设为x。
3. 插入
3.1 插入流程
红黑树的插入操作如下:
- 1) 找到插入结点的位置,即找到插入结点的父结点;
- 2) 与父结点的值进行比较,将结点插入到左结点或右结点;
- 3)插入结点颜色设置为红色,对红黑树进行修复。
插入结点为什么设置为红色?主要是因为插入结点为红色,有可能违反第4条规则,如果结点为黑色,则必然会违反第5条规则。相对来说,插入结点为红色,红黑树修复的概念更低。插入的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31private void insert(RBNode<T> node) {
RBNode<T> parent = null;
RBNode<T> tmp = this.root;
// 1.找到插入的位置
while (tmp != null) {
parent = tmp;
if (node.key.compareTo(parent.key) < 0) {
tmp = tmp.left;
} else {
tmp = tmp.right;
}
}
node.parent = parent;
// 2. 判断node是插在左子节点还是右子节点
if (parent != null) {
if (node.key.compareTo(parent.key) < 0) {
parent.left = node;
} else {
parent.right = node;
}
} else {
this.root = node;
}
//3. 将它重新修复为一颗红黑树
insertFixUp(node);
}
3.2 修复流程
插入一个结点,有五种情况,分别是:
- 1) 插入结点为头结点,违背了第2条规则,直接将结点设置为黑色即可;
- 2) 插入结点的父结点为黑色,那么仍然红黑树的规则,不用修复;
- 3) 插入节点的父节点和其叔叔节点(祖父节点的另一个子节点)均为红色的;
- 4) 插入节点的父节点是红色,叔叔节点是黑色,且插入节点是其父节点的右子节点;
- 5) 插入节点的父节点是红色,叔叔节点是黑色,且插入节点是其父节点的左子节点。
下面主要对后面三种情况进行分析,现在假定第3)种情况为case1,第4)种情况为case2,第5)种情况为case3。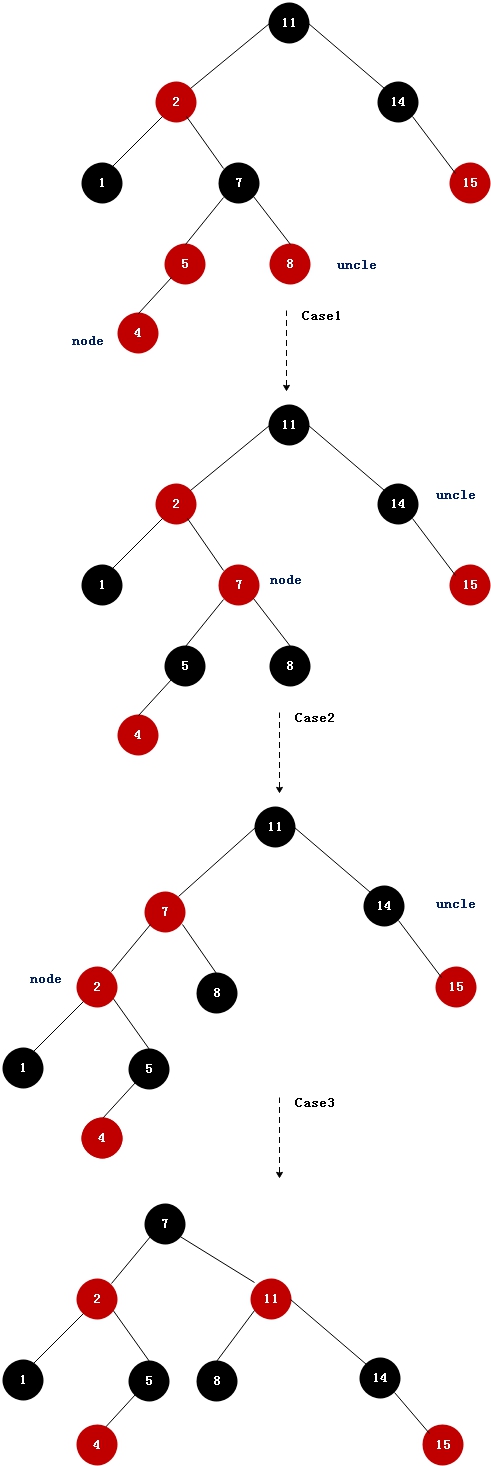
如上图所示(省略叶子结点NIL),假定当前结点为修复的结点,父结点是祖父结点的左结点(如果父结点是右结点,则与左结点是对称操作),针对这三种情况,处理办法如下:
case1: 插入节点的父节点和其叔叔节点(祖父节点的另一个子节点)均为红色
1)将父结点及叔叔结点设置为黑色;
2)祖父结点设置为红色,这样有可能改变了祖父结点的平衡。所以将当前结点结点设置为祖父结点,重新开始修复。case2: 插入节点的父节点是红色,叔叔节点是黑色,且插入节点是其父节点的右子节点
从上图可以看出,case1转换为case2,处理办法如下:
1)左旋父节点,将当前结点的父亲结点设置为当前结点,重新修复;case3: 插入节点的父节点是红色,叔叔节点是黑色,且插入节点是其父节点的左子节点
从case2转换为case3,处理办法如下:
1)将父结点设置为黑色,祖父结点设置为红色;
2)右旋祖父结点。
从上图可以看出,这三种情况是可以互相转换的,可以从case1–>case2–>case3,实际上也可能从case1–>case3,不经过case2,这要根据实际情况分析。
下面结合修复的代码分析下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87/**
* 修复红黑树
*
* @param node 修复结点
*/
private void insertFixUp(RBNode<T> node) {
// 定义父节点和祖父节点
RBNode<T> parent = null;
RBNode<T> grandParent = null;
RBNode<T> uncle = null;
// 需要修整的条件:父节点存在,且父节点的颜色是红色
while (((parent = parentOf(node)) != null) && isRed(parent)) {
// 获得祖父节点
grandParent = parentOf(parent);
// 若父节点是祖父节点的左子节点
if (parent == grandParent.left) {
// 获得叔叔节点
uncle = grandParent.right;
// case1: 叔叔节点也是红色
if (uncle != null && isRed(uncle)) {
// 把父节点和叔叔节点设置为黑色
setBlack(parent);
setBlack(uncle);
// 把祖父节点设置为红色
setRed(grandParent);
// 将当前结点放到祖父节点处
node = grandParent;
continue;
}
// case2: 叔叔节点是黑色,且当前节点是右子节点
if (node == parent.right) {
// 从父节点处左旋
leftRotate(parent);
RBNode<T> tmp = parent;
parent = node;
node = tmp;
}
// case3: 叔叔节点是黑色,且当前节点是左子节点
setBlack(parent);
setRed(grandParent);
rightRotate(grandParent);
} else { // 若父节点是祖父节点的右子节点,与上面的操作对称(左旋变右旋,右旋变左旋)
uncle = grandParent.left;
// case1: 叔叔节点也是红色
if (uncle != null && isRed(uncle)) {
// 把父节点和叔叔节点设置为黑色
setBlack(parent);
setBlack(uncle);
// 把祖父节点设置为红色
setRed(grandParent);
//将位置放到祖父节点处
node = grandParent;
continue;
}
// case2: 叔叔节点是黑色,且当前节点是右子节点
if (node == parent.left) {
// 从父节点处右旋
rightRotate(parent);
RBNode<T> tmp = parent;
parent = node;
node = tmp;
}
// case3: 叔叔节点是黑色,且当前节点是左子节点
setBlack(parent);
setRed(grandParent);
leftRotate(grandParent);
}
}
// 将根节点设置为黑色
setBlack(this.root);
}
3.3 小结
插入后的修复操作是一个向root节点回溯的操作,一旦牵涉的节点都符合了红黑树的定义,修复操作结束。之所以会向上回溯是由于case1操作会将父节点,叔叔节点和祖父节点进行换颜色,有可能会导致祖父节点不平衡(红黑树规则3),这个时候需要对祖父节点为起点进行调节(向上回溯)。祖父节点调节后如果还是遇到它的祖父颜色问题,操作就会继续向上回溯,直到root节点为止。如果上面的3种情况发生在右子树上,做相应的对称操作即可。
4. 删除
4.1 删除流程
红黑树的删除操作与平衡二叉树的删除类似,只是在平衡二叉树的基础上加入了修复的操作。与平衡二叉树的删除一样,删除操作分为三情况,1)删除结点没有子结点;2)删除结点只有一个子结点(左/右结点);3)删除结点有两个子结点。其中第三种情况可以转换为删除其右子树最小结点来实现,而最小结点只有两种情况,要么没有子结点,要么只有右子结点,从而将第三种情况转换为1)2)两情况情况。删除结点操作主要是通过改变子结点与父结点的指针来实现,如下代码所示。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67/**
* 删除分3种情况:
* 1)没有子结点;
* 2)只有一个子结点(左/右结点);
* 3)有两个子结点;
* 1)2)两种情况删除的是结点本身,
* 3)情况转换为删除其右子结点的后继结点(即右子树的最小结点),
* 在这种情况下,其后继结点左子结点为空,右子结点可不为空。
*
* @param node
*/
public void remove(RBNode<T> node) {
RBNode<T> candidate = null; // 表示删除的结点
RBNode child = null;
RBNode parent = null;
boolean color;
// 1. 寻找要删除的结点
// 1.1 没有子结点或只有一个结点,删除结点本身
if (node.left == null || node.right == null) {
candidate = node;
} else { // 1.2 有两个子结点,则删除右子树最小结点
candidate = node.right;
while (candidate.left != null) {
candidate = candidate.left;
}
}
// 2. 赋值删除结点的父结点及子结点
parent = candidate.parent;
if (candidate.left != null) {
child = candidate.left;
} else {
child = candidate.right;
}
// 3. 将子结点的父结点设置为删除结点的父结点
if (child != null) {
child.parent = parent;
}
// 4. 将父结点的子结点设置为删除结点的子结点
if (parent == null) {
this.root = child;
} else {
if (candidate == parent.left) {
parent.left = child;
} else {
parent.right = child;
}
}
// 5. 如果删除结点有两个子结点,删除其右子树最小结点之后,
// 需要将其最小结点的值赋值给删除结点,从而达到删除结点的目的。
if (candidate != node) {
node.key = candidate.key;
}
// 如果删除结点是黑色,则需要修复红黑树。
if (candidate.color == BLACK) {
removeFixUp(child, parent);
}
node = null;
}
4.2 修复流程
删除结点是黑色的,就意味着原有平衡的路径上少了一个黑色结点,违反了红黑树的第5)条规则。为了保持平衡,兄弟子树上同样必须少一个黑色结点,如此操作之后,可能导致红黑树不平衡,就只能往上追溯,将每一级的黑节点数减去一个,使得整棵树符合红黑树的定义。
修复操作分为四种情况:
- 1)调整结点节点的兄弟节点颜色是红色;
- 2)调整节点的兄弟节点颜色是黑色,且兄弟节点的子节点都是黑色的;
- 3)调整节点的兄弟节点颜色是黑色,且兄弟节点的左子节点是红色的,右节点是黑色的,如果兄弟在左边的话,则右子结点是红色的,左子结点是黑色的;
- 4)调整节点的兄弟节点颜色是黑色,且兄弟节点的右子节点是是红色的,左子节点任意颜色,如果兄弟在左边的话,则左子结点是红色的。
在删除修复的操作中,实际有八种情况,调整结点是父结点的左/右子结点,各有四种情况,不过它们的操作是对称的,我们就以调整结点是左子结点为例介绍修复操作。
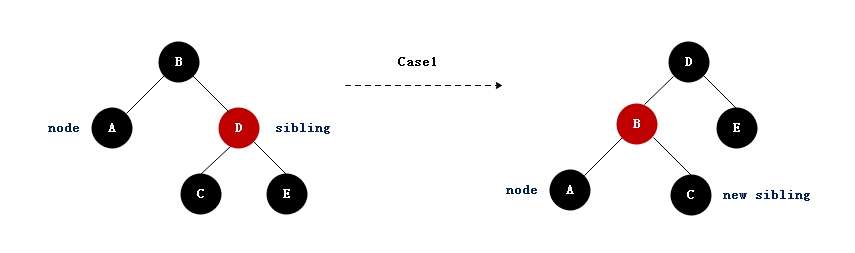
case1: 调整节点的兄弟节点颜色是红色
- 1)兄弟结点设置为黑色,父结点设置为红色;
- 2)左旋父结点;
- 3)将兄弟结点重新设置为父结点的右子结点。
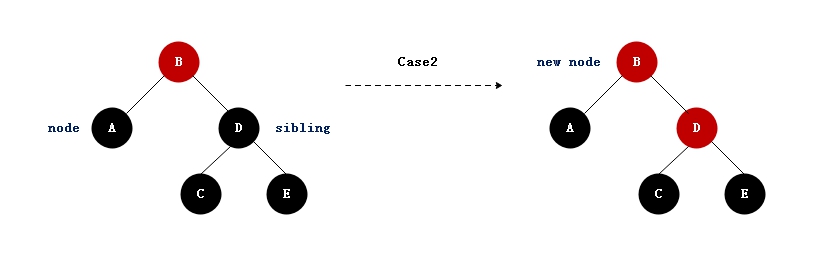
case2: 调整节点的兄弟节点颜色是黑色,且兄弟节点的子节点都是黑色的
- 1)兄弟结点设置为红色;
- 2)将调整结点设置为父结点,从父结点重新开始调整;
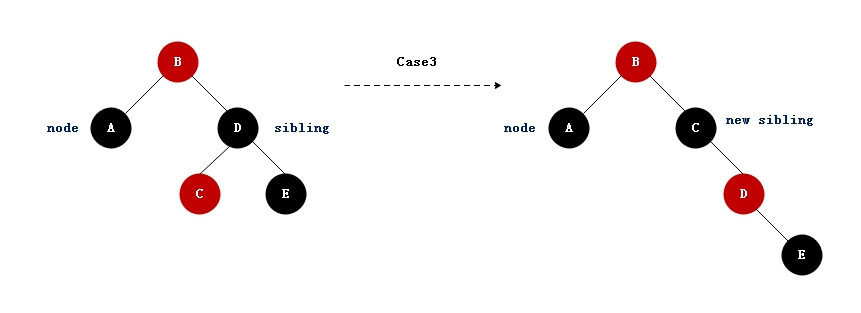
case3: 调整节点的兄弟节点颜色是黑色,且兄弟节点的左子节点是红色的,右节点是黑色的
- 1)兄弟结点的左子结点设置为黑色,兄弟结点设置为红色;
- 2)右旋兄弟结点;
- 3)兄弟结点设置为父结点的右子结点。
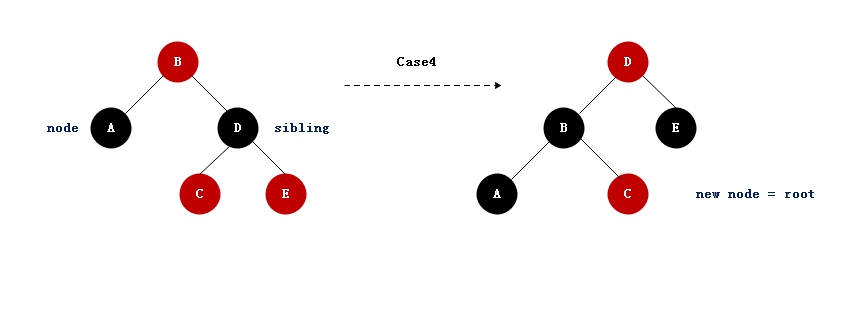
case4: 调整节点的兄弟节点颜色是黑色,且兄弟节点的右子节点是是红色的
- 1)兄弟结点颜色设置为父结点的颜色;
- 2)父结点设置为黑色;
- 3)兄弟结点的右子结点设置为黑色;
- 4)左旋父结点;
- 5)调整结点设置为根结点,从根据结点开始调整。
实现代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81/**
* 修复删除结点后的红黑树
* @param node 调整的结点(删除结点的子结点)
* @param parent 删除结点的父结点
*/
private void removeFixUp(RBNode<T> node, RBNode<T> parent) {
RBNode<T> sibling;
while ((node == null || isBlack(node)) && (node != this.root)) {
if (parent.left == node) { //node是左子节点,
sibling = parent.right; //node的兄弟节点
if (isRed(sibling)) { //case1: node的兄弟节点other是红色的
setBlack(sibling);
setRed(parent);
leftRotate(parent);
sibling = parent.right;
}
// case2: node的兄弟节点other是黑色的,且other的两个子节点也都是黑色的
if ((sibling.left == null || isBlack(sibling.left)) &&
(sibling.right == null || isBlack(sibling.right))) {
setRed(sibling);
node = parent;
parent = parentOf(node);
} else {
// case3: node的兄弟节点other是黑色的,且other的左子节点是红色,右子节点是黑色
if (sibling.right == null || isBlack(sibling.right)) {
setBlack(sibling.left);
setRed(sibling);
rightRotate(sibling);
sibling = parent.right;
}
// case4: node的兄弟节点other是黑色的,且other的右子节点是红色,左子节点任意颜色
setColor(sibling, colorOf(parent));
setBlack(parent);
setBlack(sibling.right);
leftRotate(parent);
node = this.root;
break;
}
} else { //与上面的对称
sibling = parent.left;
if (isRed(sibling)) {
// Case 1: node的兄弟other是红色的
setBlack(sibling);
setRed(parent);
rightRotate(parent);
sibling = parent.left;
}
if ((sibling.left == null || isBlack(sibling.left)) &&
(sibling.right == null || isBlack(sibling.right))) {
// Case 2: node的兄弟other是黑色,且other的俩个子节点都是黑色的
setRed(sibling);
node = parent;
parent = parentOf(node);
} else {
if (sibling.left == null || isBlack(sibling.left)) {
// Case 3: node的兄弟other是黑色的,并且other的左子节点是红色,右子节点为黑色。
setBlack(sibling.right);
setRed(sibling);
leftRotate(sibling);
sibling = parent.left;
}
// Case 4: node的兄弟other是黑色的;并且other的左子节点是红色的,右子节点任意颜色
setColor(sibling, colorOf(parent));
setBlack(parent);
setBlack(sibling.left);
rightRotate(parent);
node = this.root;
break;
}
}
}
if (node != null)
setBlack(node);
}
5. 总结
红黑树相对于AVL而言,只要经过少量的变色及旋转操作,即可实现红黑树的平衡,较好地平衡了复杂度与平衡性的关系。整个红黑树的查找,插入和删除都是O(logN)的,原因就是整个红黑树的高度是logN,查找从根到叶,走过的路径是树的高度,删除和插入操作是从叶到根的,所以经过的路径都是logN。
参考: